Simple linear ODE

1. ODE system

import numpy as np

from openmdao.api import ExplicitComponent


class SimpleLinearODESystem(ExplicitComponent):

    def initialize(self):
        self.metadata.declare('num_nodes', default=1, type_=int)

    def setup(self):
        num = self.metadata['num_nodes']

        self.add_input('y', shape=(num, 1))
        self.add_input('t', shape=num)
        self.add_output('dy_dt', shape=(num, 1))

        self.declare_partials('dy_dt', 'y', val=np.eye(num))

        self.eye = np.eye(num)

    def compute(self, inputs, outputs):
        # True solution: e^t + sin(2*pi*t)
        two_pi_t = 2 * np.pi * inputs['t']
        outputs['dy_dt'][:, 0] = inputs['y'][:, 0] + 2 * np.pi * np.cos(two_pi_t) - np.sin(two_pi_t)

    def compute_partials(self, inputs, partials):
        two_pi_t = 2 * np.pi * inputs['t']
        partials['dy_dt', 't'] = self.eye \
            * (-(2 * np.pi) ** 2 * np.sin(two_pi_t) - 2 * np.pi * np.cos(two_pi_t))

2. ODEFunction

import numpy as np

from ozone.api import ODEFunction
from ozone.tests.ode_function_library.simple_linear_sys import SimpleLinearODESystem


class SimpleLinearODEFunction(ODEFunction):

    def initialize(self):
        self.set_system(SimpleLinearODESystem)
        self.declare_state('y', 'dy_dt', targets='y')
        self.declare_time(targets='t')

    def get_test_parameters(self):
        t0 = 0.
        t1 = 1.
        initial_conditions = {'y': 1.}
        return initial_conditions, t0, t1

    def get_exact_solution(self, initial_conditions, t0, t):
        # True solution: C e^t + sin(2*pi*t)
        # outputs['dy_dt'] = inputs['y'] + 2 * np.pi * np.cos(two_pi_t) - np.sin(two_pi_t)

        y0 = initial_conditions['y']
        C = (y0 - np.sin(2 * np.pi * t0)) / np.exp(t0)
        return {'y': C * np.exp(t) + np.sin(2 * np.pi * t)}

3. Run script and output

import numpy as np
import matplotlib.pyplot as plt
from openmdao.api import Problem
from ozone.api import ODEIntegrator
from ozone.tests.ode_function_library.simple_linear_func import SimpleLinearODEFunction

ode_function = SimpleLinearODEFunction()

t0 = 0.
t1 = 1.
initial_conditions = {'y': 1.}

num = 100

times = np.linspace(t0, t1, num)

method_name = 'RK4'
formulation = 'solver-based'

integrator = ODEIntegrator(ode_function, formulation, method_name,
    times=times, initial_conditions=initial_conditions,
)

prob = Problem(integrator)
prob.setup()
prob.run_model()

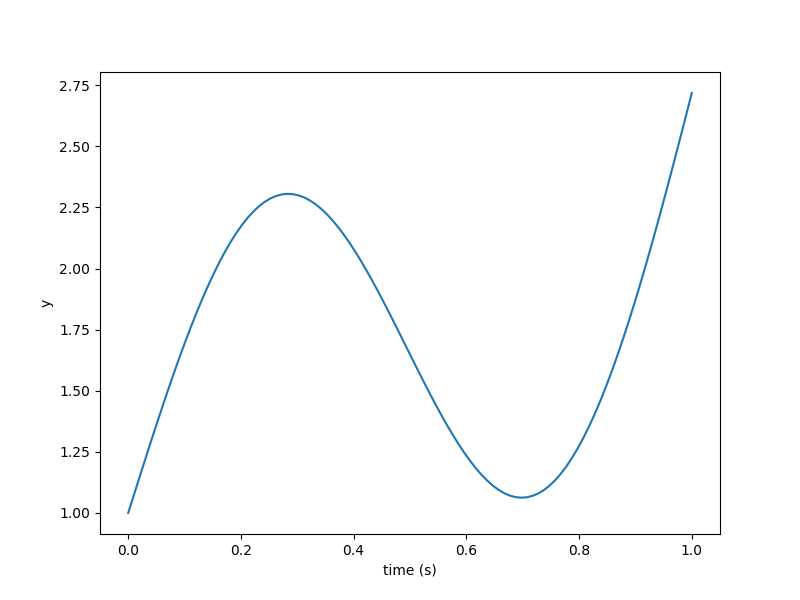
plt.plot(prob['times'], prob['state:y'])
plt.xlabel('time (s)')
plt.ylabel('y')
plt.show()

=================
integration_group
=================
NL: NLBGS 0 ; 90.2592287 1
NL: NLBGS 1 ; 12.4892941 0.138371381
NL: NLBGS 2 ; 5.40902531 0.0599276705
NL: NLBGS 3 ; 2.54497707 0.0281963086
NL: NLBGS 4 ; 0.783645137 0.0086821608
NL: NLBGS 5 ; 0.175877216 0.00194857876
NL: NLBGS 6 ; 0.0312245941 0.000345943506
NL: NLBGS 7 ; 0.00461052713 5.10809498e-05
NL: NLBGS 8 ; 0.00058493123 6.48056978e-06
NL: NLBGS 9 ; 6.52166781e-05 7.22548587e-07
NL: NLBGS 10 ; 6.49652087e-06 7.19762507e-08
NL: NLBGS 11 ; 5.85520053e-07 6.48709347e-09
NL: NLBGS 12 ; 4.82233488e-08 5.34276102e-10
NL: NLBGS 13 ; 3.65867769e-09 4.053522e-11
NL: NLBGS 14 ; 2.57417044e-10 2.85197478e-12
NL: NLBGS 15 ; 1.68904109e-11 1.87132231e-13
NL: NLBGS Converged