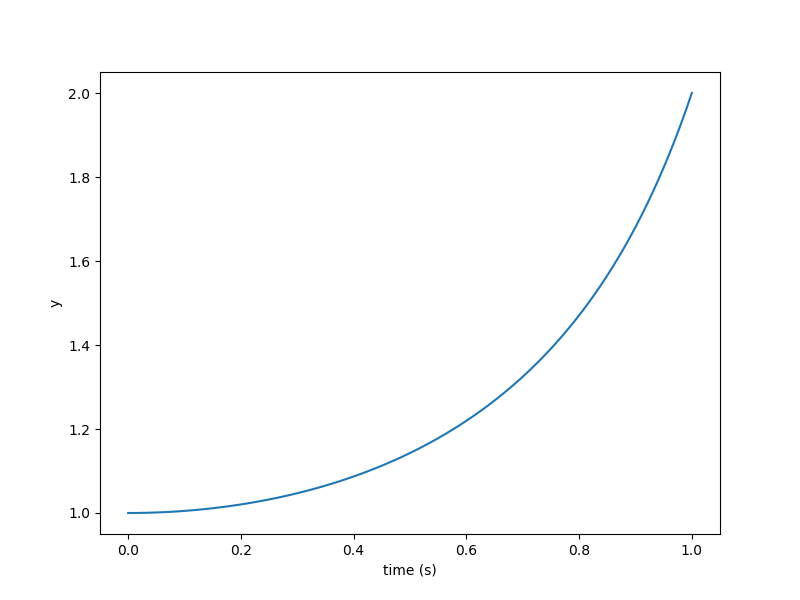
Simple nonlinear ODE

1. ODE system

import numpy as np

from openmdao.api import ExplicitComponent


class SimpleNonlinearODESystem(ExplicitComponent):

    def initialize(self):
        self.metadata.declare('num_nodes', default=1, type_=int)

    def setup(self):
        num = self.metadata['num_nodes']

        self.add_input('y', shape=(num, 1))
        self.add_input('t', shape=num)
        self.add_output('dy_dt', shape=(num, 1))

        # self.declare_partials('dy_dt', 'y', val=np.eye(num))
        self.declare_partials('dy_dt', 't', rows=np.arange(num), cols=np.arange(num))
        self.declare_partials('dy_dt', 'y', rows=np.arange(num), cols=np.arange(num))

        self.eye = np.eye(num)

    def compute(self, inputs, outputs):
        # True solution: 2 / (2*C1 - x^2)
        outputs['dy_dt'][:, 0] = inputs['t'] * np.square(inputs['y'][:, 0])

    def compute_partials(self, inputs, partials):
        partials['dy_dt', 'y'] = (2*inputs['t']*inputs['y'][:, 0]).squeeze()
        partials['dy_dt', 't'] = np.square(inputs['y'][:, 0]).squeeze()

2. ODEFunction

import numpy as np

from ozone.api import ODEFunction
from ozone.tests.ode_function_library.simple_nonlinear_sys import SimpleNonlinearODESystem


class SimpleNonlinearODEFunction(ODEFunction):

    def initialize(self):
        self.set_system(SimpleNonlinearODESystem)
        self.declare_state('y', 'dy_dt', targets='y')
        self.declare_time(targets='t')

    def get_test_parameters(self):
        t0 = 0.
        t1 = 1.
        initial_conditions = {'y': 1.}
        return initial_conditions, t0, t1

    def get_exact_solution(self, initial_conditions, t0, t):
        # True solution: 2 / (2*C - t^2)
        # outputs['dy_dt'] = inputs['t'] * np.square(inputs['y'])

        y0 = initial_conditions['y']
        C = (2. / y0 + t0 ** 2) / 2.
        return {'y': 2. / (2. * C - t ** 2)}

3. Run script and output

import numpy as np
import matplotlib.pyplot as plt
from openmdao.api import Problem
from ozone.api import ODEIntegrator
from ozone.tests.ode_function_library.simple_nonlinear_func import \
    SimpleNonlinearODEFunction

ode_function = SimpleNonlinearODEFunction()

t0 = 0.
t1 = 1.
initial_conditions = {'y': 1.}

num = 100

times = np.linspace(t0, t1, num)

method_name = 'RK4'
formulation = 'solver-based'

integrator = ODEIntegrator(ode_function, formulation, method_name,
    times=times, initial_conditions=initial_conditions,
)

prob = Problem(integrator)
prob.setup()
prob.run_model()

plt.plot(prob['times'], prob['state:y'])
plt.xlabel('time (s)')
plt.ylabel('y')
plt.show()

=================
integration_group
=================
NL: NLBGS 0 ; 16.2481804 1
NL: NLBGS 1 ; 8.99057129 0.553327884
NL: NLBGS 2 ; 5.25549451 0.323451265
NL: NLBGS 3 ; 2.3091862 0.14211968
NL: NLBGS 4 ; 0.78372072 0.0482343684
NL: NLBGS 5 ; 0.212933 0.0131050367
NL: NLBGS 6 ; 0.0479807709 0.00295299348
NL: NLBGS 7 ; 0.00923486381 0.000568362953
NL: NLBGS 8 ; 0.00155294802 9.55767344e-05
NL: NLBGS 9 ; 0.000232098823 1.4284604e-05
NL: NLBGS 10 ; 3.12388759e-05 1.92260765e-06
NL: NLBGS 11 ; 3.82602625e-06 2.35474136e-07
NL: NLBGS 12 ; 4.3003494e-07 2.64666522e-08
NL: NLBGS 13 ; 4.46693954e-08 2.74919371e-09
NL: NLBGS 14 ; 4.3135972e-09 2.65481863e-10
NL: NLBGS 15 ; 3.89222605e-10 2.39548426e-11
NL: NLBGS 16 ; 3.29592108e-11 2.02848626e-12
NL: NLBGS 17 ; 2.62811994e-12 1.6174857e-13
NL: NLBGS Converged